Skip to main content
Alnur Ismail - Founder, Advisor, Investor
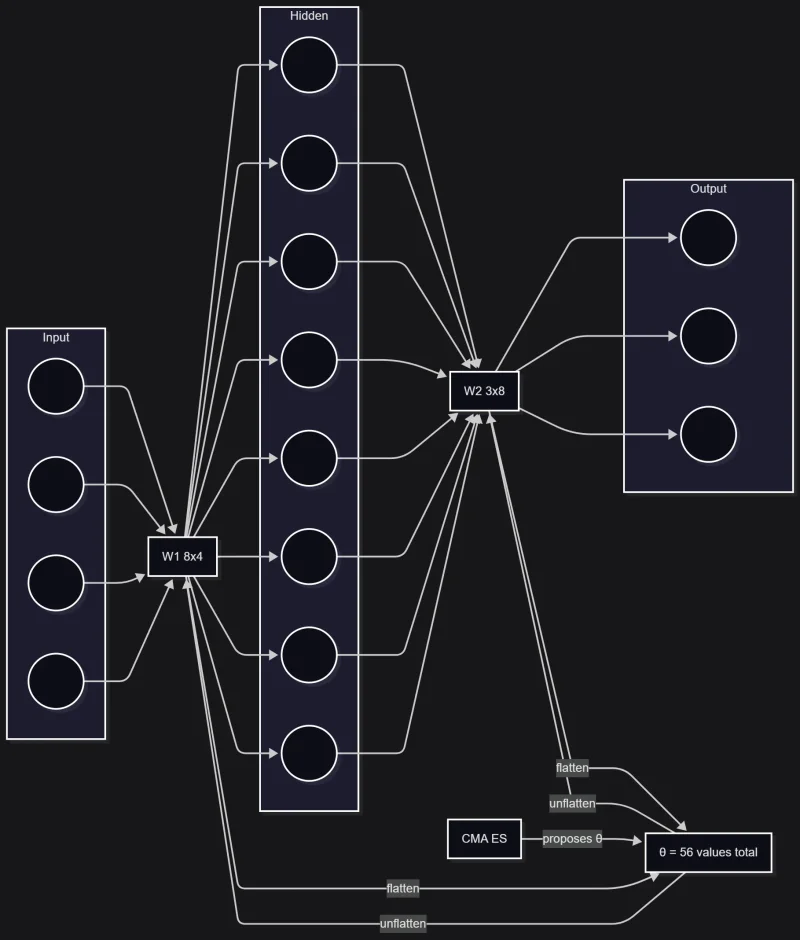
Featured image for post: Multilayer CMA-ES

Multilayer CMA-ES

• 1 min
CMA-ES ES

What I worked on

Creating a MLP that uses the CMA-ES to optimize a non-linear policy

graph LR

    %% --------------------------
    %% ORIGINAL MLP
    %% --------------------------

    subgraph Features
        A1(( ))
        A2(( ))
        A3(( ))
        A4(( ))
    end

    W1[ W1 8x4 ]

    subgraph Hidden
        H1(( ))
        H2(( ))
        H3(( ))
        H4(( ))
        H5(( ))
        H6(( ))
        H7(( ))
        H8(( ))
    end

    W2[ W2 3x8 ]

    subgraph Actions
        O1(( ))
        O2(( ))
        O3(( ))
    end

    A1 --> W1
    A2 --> W1
    A3 --> W1
    A4 --> W1

    W1 --> H1
    W1 --> H2
    W1 --> H3
    W1 --> H4
    W1 --> H5
    W1 --> H6
    W1 --> H7
    W1 --> H8

    H1 --> W2
    H2 --> W2
    H3 --> W2
    H4 --> W2
    H5 --> W2
    H6 --> W2
    H7 --> W2
    H8 --> W2

    W2 --> O1
    W2 --> O2
    W2 --> O3


    %% --------------------------
    %% FLATTEN + CMA ES SECTION
    %% --------------------------

    W1 -- flatten --> THETA[θ = 56 values total]
    W2 -- flatten --> THETA

 
    CMA[CMA ES]

    CMA -- proposes θ --> THETA
    THETA -- unflatten --> W1
    THETA -- unflatten --> W2

What I noticed

  • Can use pytorch to create the same network architecture - just turn off grads
  • All layer weights get flattened and CMA-ES learns the non-linear policy
  • As expected it learnt a better policy. When full it NOOPs vs FORWARD getting better survival.

”Aha” Moment

  • CMA-ES is just an optimization strategy for the weights vector
  • It’s black box because it does’t care about the network layers or activations. It never sees it. Just a flattened weight vector

What still feels messy

n/a

Next step

Add JUMP action for final policy, then getting back to continuous learning.