Covariance Matrix and Distribution

What I worked on

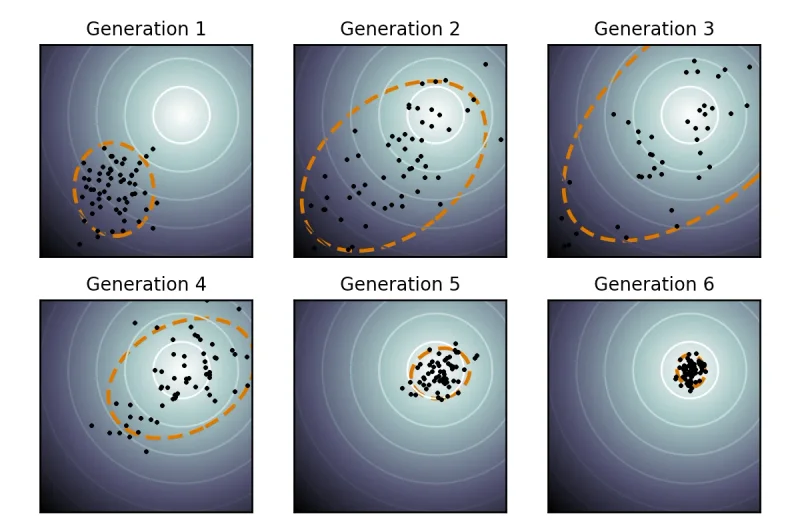
Tried to understand covariance matrix adaptation in evolution strategies and how populations are represented as multivariate Gaussians. Compared CMA-ES and NES approaches.

What I noticed

• CMA-ES tracks full covariance to shape sampling
• NES uses stochastic gradients for population updates
• Isotropic Gaussian means equal variance in all directions
• Perturbing parameter space is different from action space
• CMA-ES and NES are related families of methods

”Aha” Moment

That the covariance matrix captures dependencies between parameters so the algorithm learns sampling direction, not just magnitude.

What still feels messy

How energy-based models might compare.

Next step

Code a small CMA-ES example to visualize the evolving covariance ellipse.